nitrosite.blogg.se - Pandas plot scatter jitter

#Pandas plot scatter jitter code#

SPSS’s default smoothing is alittle too smoothed for my taste, so I set the proportion of the X variable to use in estimating the mean within the position statement. GUIDE: axis(dim(2), label("Y"), delta(0.2), start(0))ĮLEMENT: line(position(smooth.loess(X*Y, proportion(0.2))), color(color.red))ĮLEMENT: line(position(X*ActualFunct), color(color.blue)) GRAPHDATASET NAME="graphdataset" VARIABLES=X Y YJitt ActualFunctĭATA: ActualFunct=col(source(s), name("ActualFunct")) Loess was originally meant for continuous data, but for exploratory analysis it works just fine on the 0-1 data here. It does a pretty good job of identifying the discontinuity at 0.8, but the change points earlier are not visible. The red line is the smoother, and the blue line is the actual proportion I generated the fake data from. No binning necessary, here is an example using loess right within the GGRAPH call. But since I draw the Y axis as continuous here I can do the jittering myself.Ī useful tool for exploratory data analysis is to add a smoothing term to plot – a local estimate of the mean at different locations of the X-axis.

#Pandas plot scatter jitter code#

If I made the Y axis categorical I would need to use point.jitter in the inline GPL code because SPSS will always force the categories to the same spot on the axis.

Transparency.exterior(transparency."0.7")) GRAPHDATASET NAME="graphdataset" VARIABLES=X Y YJittĭATA: YJitt=col(source(s), name("YJitt")) *Making a jittered chart.ĬOMPUTE YJitt = RV.UNIFORM(-0.04,0.04) + Y. The extra aesthetic options for making points smaller and semi-transparent are at the end of the ELEMENT statement. SPSS can jitter the points directly within GGRAPH code (see point.jitter), but here I jitter the data slightly myself a uniform amount.

draw the points smaller and slightly transparent.

jitter the points slightly on the Y-axis so they don’t overlap.

So here we will do a few things to the chart to make it easier to interpret: GRAPHDATASET NAME="graphdataset" VARIABLES=X Y Here is the fake data I made and the GGRAPH code to make said chart. J Physiol 589:1861-3.Oh boy, that is not helpful. And the good news is that the people behind Python’s Seaborn and R’s ggplot2 have done the hard work for us. Try adding individual data points and jitter to your next figures, your readers will be grateful. Jitter can easily be added to plotted data to make nice plots like this one and this one. The module contains a function called _jitter() that adds jitter to the data to be plotted (I wrote this before I knew about Seaborn!).Ĭreating pretty, informative plots is one of the hallmarks of ggplot2, a plotting system for the R statistical programming language. I have written a small Python module to generate plots for paired data and their difference. The code used to generate this figure is available here. The next two subplots show two ways to add jitter in Python with the Seaborn statistical plotting package.

Because the first subplot does not include jitter, it is difficult to tell whether some data points overlap. The following figure has three subplots that all include individual data points. Jitter is simply the addition of a small amount of horizontal (or vertical) variability to the data in order to ensure all data points are visible.

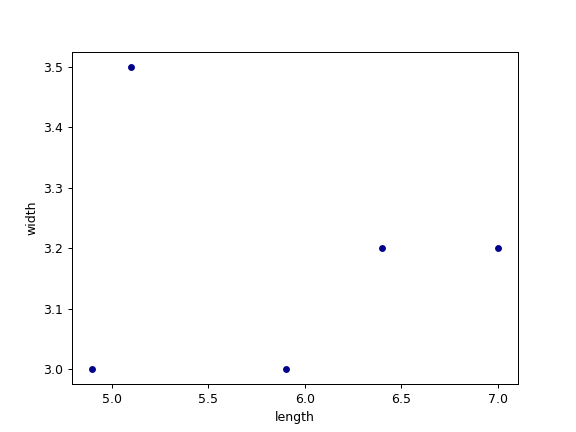
This can easily be solved by adding some jitter to the individual points that have the same or similar values.

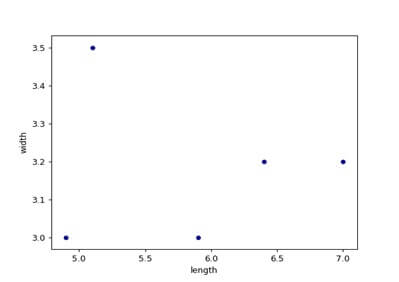
One problem with plotting individual data points is that they can overlap and make it difficult to see all of the data. Using jitter to help readers see your data As highlighted in our previous posts, scientists are encouraged to plot the data used to compute the summary statistics in figures (e.g., Drummond & Vowler, 2011). can be misleading and conceal the nature of the underlying data. Why is showing data important? As previously pointed out here and here, figures with means, standard deviations, standard errors, etc. Scientific figures are at their most informative when they include the individual data used to calculate summary statistics such as means and standard deviations.